-1장 컴퓨터 내부의 언어 체계

언어란 무엇인가?

언어는 정보를 서로 소통하기 위해 만들어 졌다. 

모든 언어의 뜻은 기호의 집합으로 인코딩(encoding)된다. 하지만 의미를 기호로 인코딩하는 것만으로는 충분하지 않다.

언어가 제대로 작동하려면 의사소통하는 당사자들이 모두 같은 문맥context을 공유해서 같은 기호에 같은 뜻을 부여할 수 있어야 한다.

 

비트

'비트' 라는 단어는 2진법을 사용한다는 뜻의 '바이너리'(bubary)와 숫자를 뜻하는 '디지트'(eigit)가 기묘하게 합쳐진 말

비트는 2진법을 사용한다. 

 

논리연산

비트 사용법 중 하나는 예/아니요 질문에 대한 답을 표현하는 것. 이때 예를 '참'(True) 아니요를 '거짓'(false)이라는 용어로 부른다. 그러나 예/아니요는 모든 질문에 대답을 할 수가 없다. 이러한 대답을 하기 위해

다른 비트들이 표현하는 내용으로부터 새로운 비트를 만들어내는 이런 동작을 논리 연산(logic operation)이라고 한다.

 

불리언 대수

대수가 수에 대한 연산 규칙의 집합인 것처럼. 1800년대 영국 수학자 조지 불이 만들어낸 불리언 대수도 비트에 대해 사용할 수 있는 연산 규칙의 집합이다. 일반 대수와 마찬가지로 결합,교환,분배법칙을 적용할 수 있다.

기본적인 불리언 연산자는 NOT, AND, OR세가지다 추가로 XOR이라는 합성연산이 있다.

 

NOT : 이 연산은 '논리적 반대'를 의미한다. 거짓인 비트에 NOT을 더하면 참. 참인 비트에 NOT을 더하면 거짓

AND : 이 연산은 둘 이상의 비트에 작용한다. 2비트 연산인 경우 두 비트가 모두 참일 경우에만 결과가 참이 된다.

OR : 이 연산도 둘 이상의 비트에 작용한다. 2비트 연산인 경우 두 비트중 하나만이라도 참이면 결과가 참이 된다.

XOR: 베타적(exclusive)OR은 두 비트의 값이 서로 다를경우에만 참이 된다.

 

드모르간의 법칙

정수를 비트로 표현하는 방법

더 고차원으로 올라가서 비트를 사용해 수를 표현하는 방법을 알아보자.

 

양의 정수 표현

우리는 보통 10진수 체계를 사용한다.

10진수 체계에서는 10가지 기호인 숫자를 상자에 담을 수 있다. 이때 오른쪽에서 왼쪽으로 상자가 쌓여가며 각 상자마다 각기 다른 이름이 붙어있다.

맨오른쪽에서부터 일의자리, 십의자리, 백의자리 ... 각 이름은 10의 거듭제곱에 해당한다 즉 10^0은 1, 10^1은 10, 10^2는 100...이 체계는 지수를 적용한 밑으로 10을 사용하기에 10진수라 불린다.

 

비트를 사용해 값을 만들 때도 이와 비슷하게 접근할 수 있다. 10진 숫자 대신 비트를 사용하기 때문에 각 상자에 사용할 기호는 1과 0 두가지밖에 없다. 이를 10진수와 마찬가지로 2진수 즉 밑을 2로 대신하여 계산을 하면 된다.

0000을 2진법으로 계산하면 2^3*0+2^2*0+2^1*0+2^0*1=0

0011을 2진법으로 계산하면 2^3*0+2^2*0+2^1*1+2^0*1=0

1110을 2진법으로 계산하면 2^3*1+2^2*1+2^1*1+2^0*0=15다.

 

조금 더 큰수인 5028을 어떻게 2진수로 쓸 수 있는지 생각해보자

5028은 각각의 자리들이 모여 1001110100100이라는 2진수를 이루고 총 13개의 비트를 가지고 있어 13비트수를 가지고 있다.

 

10진수의 숫자 개수는 표현할 수 있는 값의 범위를 결정한다. 예를 들어 0~99 사이의 100가지 다른 수를 10진 숫자 2 개로 표현할 수 있다. 마찬가지로 2진수에서도 비트의 개수가 표현할 수 있는 값의 범위를 결정한다.

예를 들어 2비트만 사용하면 0~3 사이에 속하는 네가지 수를 표현할 수 있다. 

비트 개수	값의 개수	값의 범위
4	16	0....15
8	256	0.....255
12	4,096	0....4096
16	65,536	0...65535
20	1,048,576	0....1048575
24	16,777,216	0....16777215
32	4,294,967,296	0....4294967295
64	18,446,744,073,709,551,616	0....18446744073709551615

2진수에서 가장 오른쪽의 비트를 가장 작은 유효비트 라고 부르고 가장 왼쪽의 비트를 가장 큰 유효비트 라고 부른다.

가장 오른쪽의 비트를 변경하면 2진수의 값이 가장 작게 변경되고 가장 왼쪽의 비트를 변경하면 2진수의 값이 가장 크게 변하기 때문에 이런 이름이 붙었다.

 

컴퓨터를 사용하는 사람들은 종종 세글자 줄임말을 사용하기 때문에 가장 작은 유효비트, 가장 큰 유효비트를 각각 LSB와 MSB라고 부른다.

 

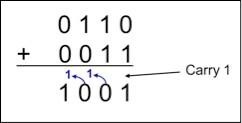
2진수 덧셈

0 + 0 = 0
0 + 1 = 1
1 + 0 = 1
1 + 1 = 10

 

A	B	A AND B	A + B	A XOR B	A	B
0	0	0	00	0	0	0
0	1	0	01	1	0	1
1	0	0	01	1	1	0
1	1	1	10	0	1	1

컴퓨터가 덧셈을 사용할 땐 다음과 같은 규칙으로 계산한다.

두 비트를 서로 더한 결과는 두 비트를 XOR 한 값과 같고, 올림은 두 비트를 AND한 값과 같다.

 

덧셈 결과가 우리가 사용할 비트의 개수로 표현할 수 있는 범위를 벗어나면 어떻게 해야 할까?

이런 경우 오버플로가 발생한다. 오버플로란 말은 MSB에서 올림이 발생했다는 뜻이다.

 

컴퓨터에는 조건코드(또는 상태코드) 레지스터 라는 것이 있어서 몇가지 이상한 정보를 담아둔다. 이런 정보 중에는 오버플로 비트가 있고 이 비트에는 MSB에서 발생한 올림값이 들어간다. 이 비트값을 보면 오버플로가 발생했는지 알 수 있다.

음수 표현

앞에서 살펴본 모든 2진수는 양수였다. 그러나 실제 세계에서 문제를 해결하려면 양수와 음수를 모두 사용해야 하는 경우가 많다. 

 

음수와 양수를 구별하기 위해 흔히 부호를 사용한다. 부호에는 양부호와 음부호라는 두가지 값이 있다.

따라서 이를 비트 하나를 써서 표현할 수 있다. 우리는 가장 왼쪽 비트(MSB)를 부호에 사용하기로 멋대로 결정했다.

따라서 4비트 중에 3비트가 남고 이를 사용하면 0부터 7까지 수를 표현할 수 있다.

부호 비트가 0이면 이 2진수를 양수로 취급하고

부호 비트가 1이면 이 2진수를 음수로 취급한다

부호	2^2	2^1	2^0	10진수
0	1	1	1	+7
0	1	1	0	+6
0	1	0	1	+5
0	1	0	0	+4
0	0	1	1	+3
0	0	1	0	+2
0	0	0	1	+1
0	0	0	0	+0
1	0	0	0	-0
1	0	0	1	-1
1	0	1	0	-2
1	0	1	1	-3
1	1	0	0	-4
1	1	0	1	-5
1	1	1	0	-6
1	1	1	1	-7

1의 보수

음수를 표현하는 또다른 방법으로는 양수의 모든 비트를 뒤집는 방법이 있다.

이를 1의 보수 표현법이라고 부른다.

부호	2^2	2^1	2^0	10진수
0	1	0	0	+4
0	0	1	1	+3
0	0	1	0	+2
0	0	0	1	+1
0	0	0	0	+0
1	1	1	1	-0
1	1	1	0	-1
1	1	0	1	-2
1	1	0	0	-3
1	0	1	1	-4
1	0	1	0	-5
1	0	0	1	-6
1	0	0	0	-7

음수에선 각 비트를 뒤집으면 그 수가 나온다 -7 -> 000 -> 111

 

현재 컴퓨터에선 1의 보수 표현법을 사용하지 않는다.

그 이유는 순환 올림을 처리하기 위한 하드웨어를 추가해야하는데 이 말은 비용이 더 든다는 뜻이기 때문이다.

 

2의 보수

특별한 하드웨어를 추가할 수 없고 XOR과 AND 연산만 사용해야 한다면 어떻게 일반 정수 사이의 덧셈을 할 수 있을까

이럴 때 2의 보수를 사용하면 된다

 

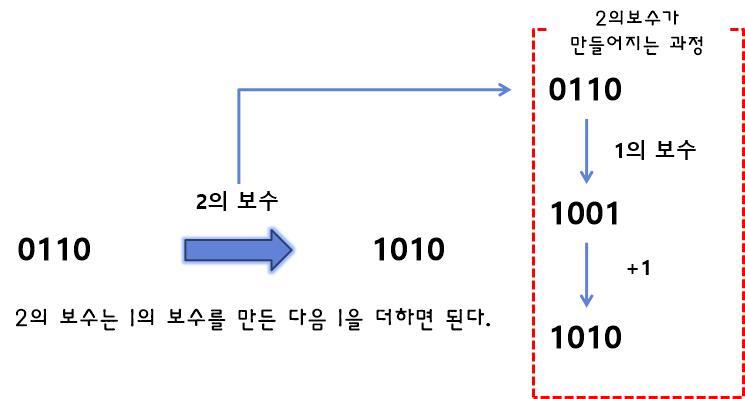
이 방법은 부호가 있는 정수를 표현할 때 가장 널리 쓰이는 방법이다. 어떤 수의 비트를 뒤집고 ( 즉 각 비트의 NOT을 계산) 1을 추가하면 음수를 얻을 수 있다. 이때 올림이 발생하면 이 값은 버린다 즉 +1 0001의 비트를 뒤집으면 1110이고

여기에 1을 더하면 1111이 되며 이 값이 -1을 표현한다.

비슷하게 +2는 0010이고 비트를 뒤집어 1을 더하면 1110이며 이값이 -2다

 

1의 보수는 0을 1로 1을 0으로 바꿔주면 완성되었다. 그렇다면 2의 보수는 모든 자리의 수가 1인 수에 1을 더한 수를 만들어 주면 된다.

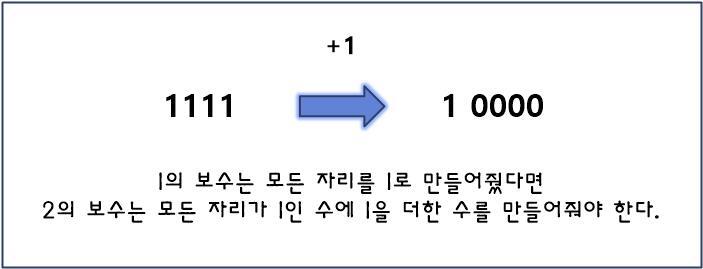
그렇기 때문에 2의 보수를 만드는 가장 쉬운 방법은 먼저 1의 보수를 만든 후 그수에 1을 더하면 2의 보수가 완성된다

부호	2^2	2^1	2^0	10진수
0	1	1	1	+7
0	1	1	0	+6
0	1	0	1	+5
0	1	0	0	+4
0	0	1	1	+3
0	0	1	0	+2
0	0	0	1	+1
0	0	0	0	+0
1	1	1	1	-1
1	1	1	0	-2
1	1	0	1	-3
1	1	0	0	-4
1	0	1	1	-5
1	0	1	0	-6
1	0	0	1	-7
1	0	0	0	-8

2의보수를 사용하면 계산을 더 쉽게 할 수 있다.  -4 + 2

1   0100

0   0010

----------

1   0110

-2는 1 0110

 

 

추가로 프로그래머들은 자신이 다뤄야 하는 수를 표현하기 위해 필요한 비트의 개수를 알 필요가 있다.

다음 표는 2의 보수를 사용해 표현할 수 있는 값의 범위를 보여준다.

비트 개수	값의 개수	값의 범위
4	16	-8....7
8	256	-128...127
12	4,096	-2048....2047
16	65,536	-32768....32767
20	1,048,576	-524288...524287
24	16,777,216	-8388608....8388607
32	4,294,967,296	-2147483648....2137483647
64	18,446,744,073,709,551,616	-9223372036854775808.... 9223372036854775807